Convexity in LDI Liabilities—How to Earn More and Be Better Hedged

Currently, when crafting LDI solutions for defined benefit (DB) schemes, the pension community tends to focus attention on matching the duration of assets with liabilities. In our recent LDI Insights, Duration Is a ZIP Code, Not an Address, my colleague Mike Bazdarich explains precisely why this is helpful yet not sufficient to address these matching needs, even in the short term. By attempting to match the duration of liabilities using fixed-income assets, a DB plan is insulating itself from some of the potential interest-rate risks. Unless it also aligns the convexity of assets with liabilities, this insulation may be very short-lived. In this brief note, we explain what convexity is, why it matters and how to help shield a plan from these often overlooked convexity risks. The good news is that a plan can even be paid to reduce these risks.

Convexity Complexity

We suspect little attention is paid to the convexity risk in DB plans and other LDI portfolios. Plan liabilities are typically positively convex—meaning that for a given level of duration, the value of liabilities will fall less when yields rise and increase more when yields fall. Essentially, being positively convex means being more right as interest rates fall and less wrong as interest rates rise. While being overweight or underweight duration is an asset allocation decision, there is no good reason for a plan with longer-dated liabilities to retain this “short convexity.” Furthermore, as we will explain later, the plan may actually be paid extra yield to remove this short position. Put simply, the fund can earn more and be better hedged.

Convexity Illustrated

Different bonds with similar durations can have very different convexities, as we demonstrate in Exhibit 1. The red bond is “highly convex,” such that the relationship between the change in price for a given increase, say 100 basis points (bps), or a decrease of the same amount in yield, is very different from that of the green bond which we’ve drawn as “low convexity.” We assume they have similar durations (in that the slope of the tangent to the curve is very close on both red and green bonds) and identical yields (y0). When we lower the yield by 100 bps (from y0), the price of the red bond rises from 100 to 110, while the green bond moves from 100 to 105. Furthermore, when yields rise by 100 bps, we can see that the red bond only falls from 100 to 98 while the green bond falls further to 97. Similar bonds will have different convexity when their coupons and maturities vary. Typically, bonds with more convexity (for a given maturity) will have a lower yield (i.e., be more valuable).

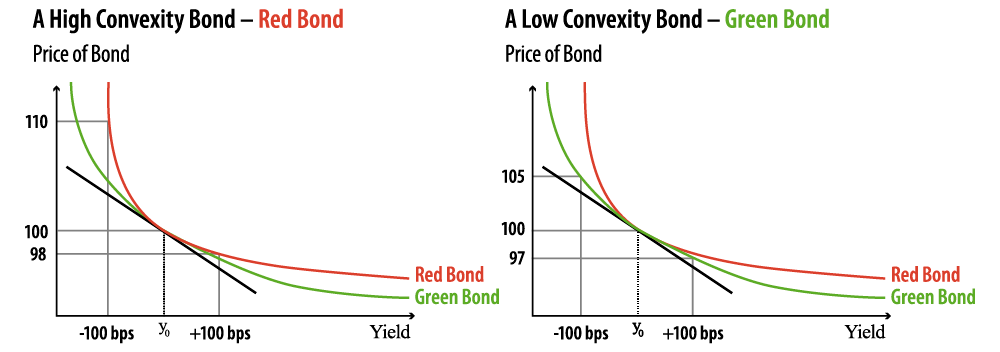
The liabilities of DB plans are “bond-like” and as such also have positive convexity, which can be high or low, just like the red and green bonds in Exhibit 1. Our example demonstrates that employing bonds that match the duration of the plan liabilities is far from enough to be confident of similar performance. If a plan is “short convexity” relative to the liabilities, we would expect that, generally, the strategy will underperform in both a rising and falling interest-rate environment, just as the green bond underperforms the red bond.

Fixing the Convexity Complexity

The underweight to convexity in LDI plans comes mostly from the liabilities with longer-dated maturities. The present value of US pension liabilities past the 30-year point is not a large part of pension liabilities (approximately 10%), but the convexity risk coming from these liabilities is thought to be between 25% and 35% of their total convexity risk. Longer-dated liabilities may represent a small part of a DB plan in terms of present value, but they represent a large proportion of a plan’s convexity risk. By simply owning more convexity, LDI managers can better track a plan’s liabilities. This is where longer-dated bonds, especially STRIPS, can come into play as they provide more convexity per unit of duration relative to shorter-duration assets.

In Exhibit 2, we show the convexity per unit of duration for the range of US Treasury (UST) maturities, together with their stripped principal bonds. You can see that by moving out the “whole bond curve,” the fund acquires convexity more efficiently—a higher amount of convexity per unit of duration. Furthermore, employing equivalent-maturity principal STRIPS achieves an even higher amount of convexity for a given amount of duration. Often (and currently), a DB plan could achieve an even higher yield by employing STRIPS for a given set of duration and convexity characteristics. Exhibit 2 illustrates this concept using option-adjusted duration (OAD) and option-adjusted convexity (OAC) of USTs.

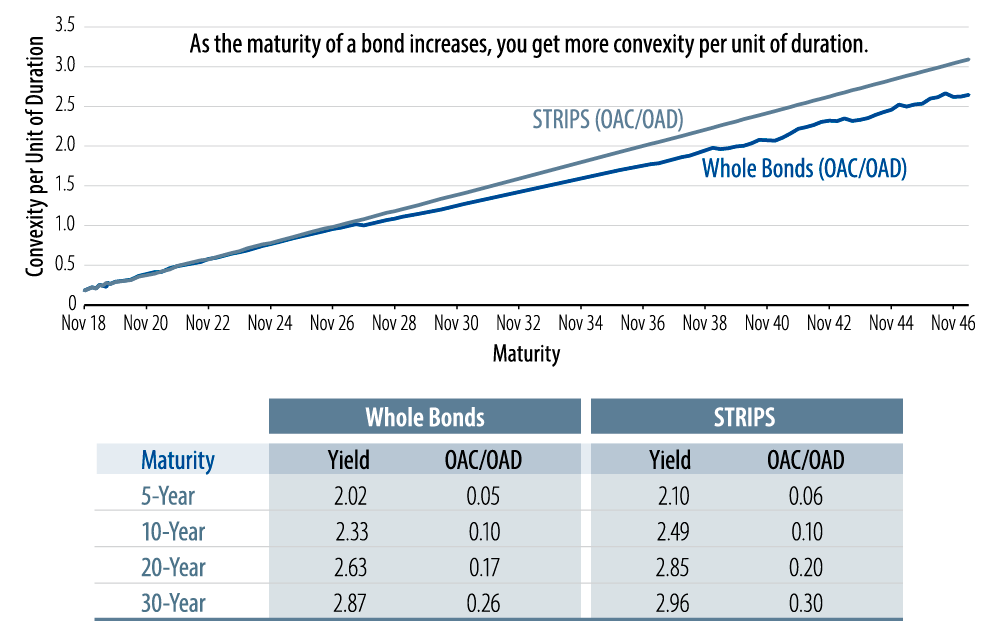
Moving further out on the yield curve is a good way to own more convexity, and it can be argued that convexity in the long end is cheap because the curve is steep and a plan doesn’t have to give up yield to own it. Essentially, being short convexity against DB plan liabilities is like being short a cheap asset that can help better track those liabilities. Thus, we feel pension funds should make a greater effort to hedge this convexity risk in any rate environment. The benefit from additional convexity appears minimal if interest rates continue in their recent narrow range. But as longer-term investors, sooner or later pension fund managers are likely to see the sort of moves in interest rates that make this benefit from convexity so apparent. The kicker is that plans are getting more yield from instruments that provide this convexity due to the yield concession implied by an upward sloping yield curve¹.

DB plan liabilities stretch far out into the future. The further out in time, the more they suffer from this convexity shortfall versus their assets. The deficiency of investable assets that mature beyond the 30-year point is one reason this convexity risk remains unhedged. To cover this shortfall, we suggest owning duration from longer maturities, as they provide some of the biggest “bang (convexity) for your buck (duration).” Not only is the DB pension community underweight convexity, it is also relatively underweight duration versus its liabilities. With bond yields low on a historical basis, we sympathize with the reticence to cover this mismatch. The optimal way to cover this shortfall relative to the liabilities would be to maximize the convexity per unit of duration. Not only does this reduce convexity and duration risks, it frees up cash to invest in other assets, as DB plans need less principal to achieve a given duration. As shown in Exhibit 3, these “freed-up funds” can be especially valuable to underfunded plans as they can be used to enhance overall portfolio returns.

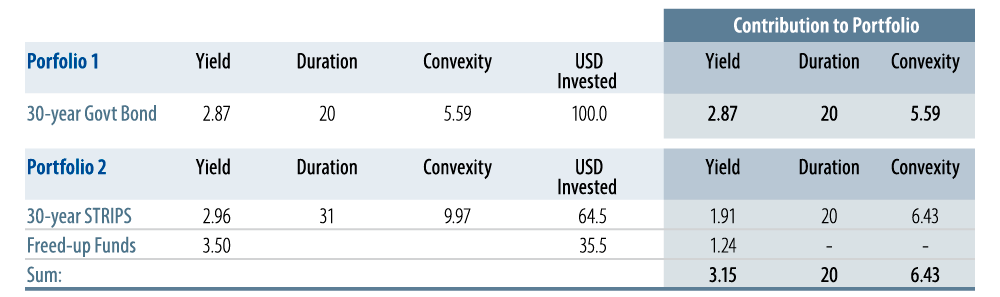
Plans can achieve the same duration and additional convexity with 64.5% of the portfolio invested in the 30-year UST STRIPS as compared with the 30-year UST whole bond. And, if a plan can earn 3.5% on the “freed-up” 35.5%², then the yield of the portfolio could be enhanced by 28 bps (3.15–2.87) and be better hedged overall.

In the case of using STRIPS to cover this shortfall, the icing on the cake is that it is the one product that does not have reinvestment risk—another often-overlooked aspect of investing. With STRIPS, the return achieved is the yield at purchase. At Western Asset, we structure our long-duration portfolios seeking to take advantage of this convexity benefit.

Conclusion

With so much focus on duration and given the low level of yields available, convexity risks in DB plans and other LDI portfolios have become an afterthought in the asset allocation process. Importantly, though, plans can reduce funded status volatility and enhance yield by simply owing convexity. Pension funds should be thrilled to own an asset that can reduce funded status volatility in both rising- and falling-rate environments. What’s even better is that doing so provides the opportunity to gain extra yield due to a relatively steep yield curve. This provides an option to reduce funded status volatility and get paid for it. The positive convexity in longer-maturity bonds and STRIPS protect pension portfolios from losing ground against the positive convexity of their liabilities.